This is a constantly evolving showcase of materials, methods, and video excerpts from my classroom. Below you will find animations, video clips, and in-class activities that I have created during my time in the beautiful, messy, and delightfully human world of teaching undergraduate mathematics.
Read more about my approach to the classroom in my Statement of Teaching Philosophy and Statement on Diversity and Inclusion.
TEACHING EXPERIENCE
Multivariable Calculus, GT, MATH-2551, Fall '21 & Spring '22
Mathematical Biology, GT, MATH-4755, Spring '21
Integral Calculus, GT, MATH-1552, Fall '20 & Spring '21
Calculus I, NCSU, MA-141, Fall '19
Calculus II, NCSU, MA-241, Spring '19 & Spring '20
Calculus III, NCSU, MA-242, Fall '18 & Summer '19
SAMPLE MATERIALS
Course Syllabus - MA141 Calculus I
Final Exam - MA242 Calculus III
Group Activity: The Cell Burst Problem
ANIMATIONS GALLERY
Technology can be an invaluable tool in helping calculus spring off the page. Calculus is fundamentally about motion and change, and the pen-and-paper calculations we perform often fail to make these concepts come to life. Below is a sample from the collection of animations that I have made during my time teaching Calculus to help difficult concepts click.
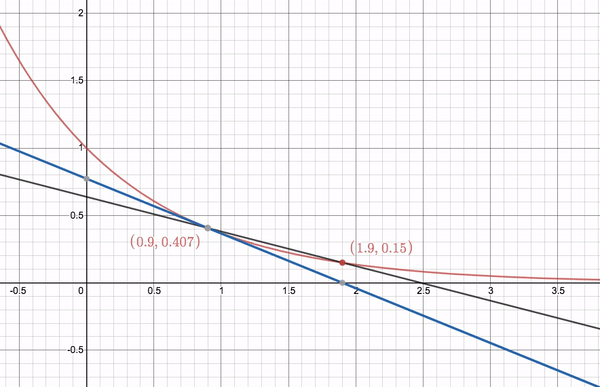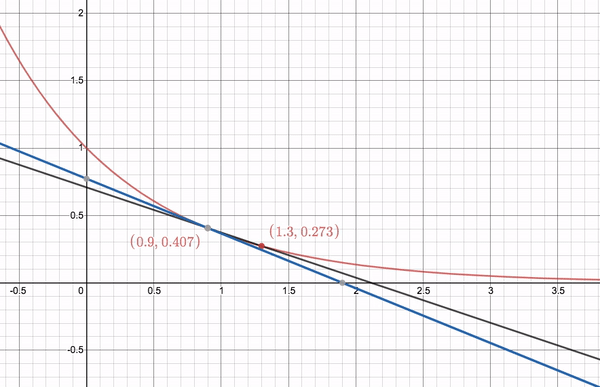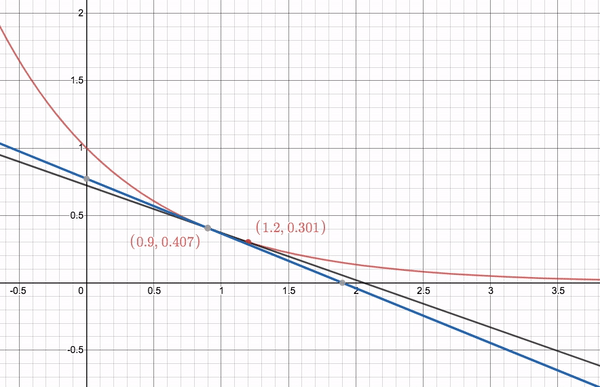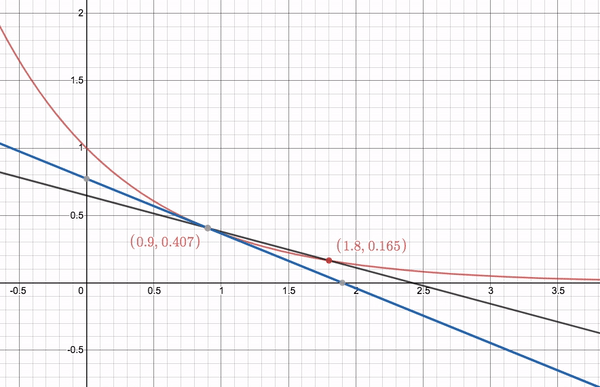
Secant lines approaching a tangent line
Newton's Method finds a root
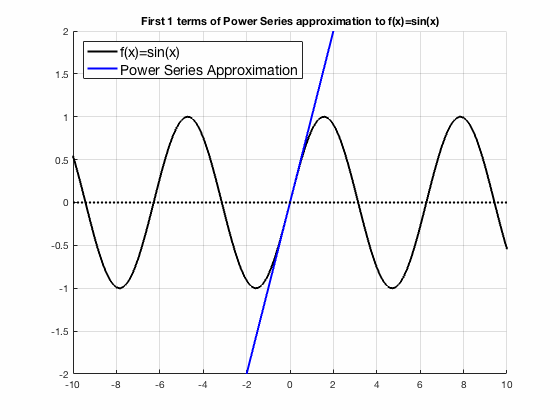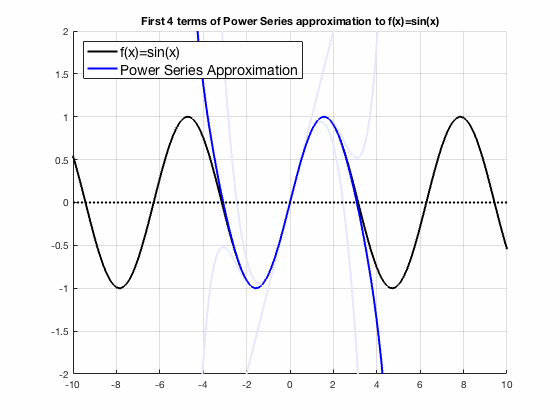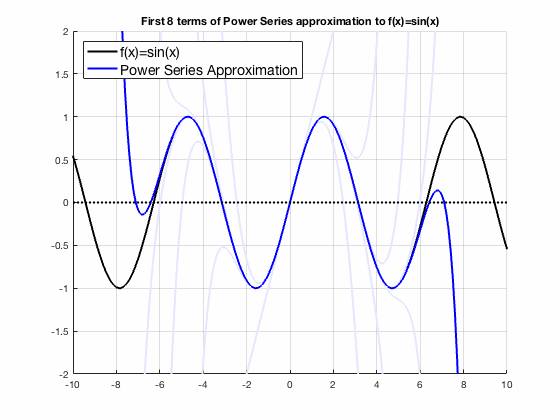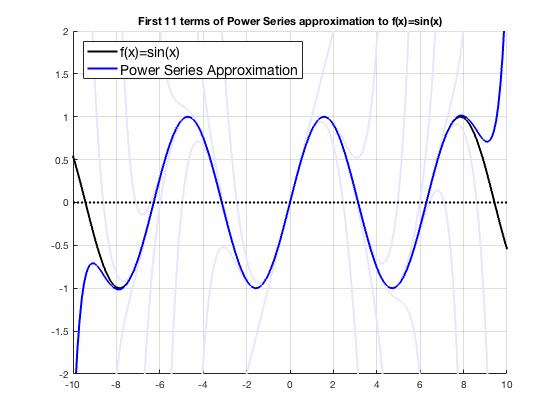
Taylor series converges to sin(x)
The Fundamental Theorem of Calculus, animated
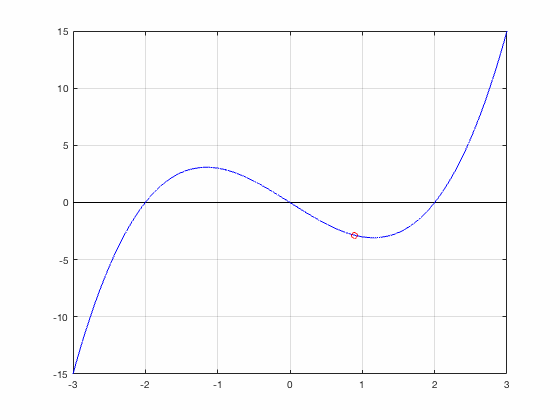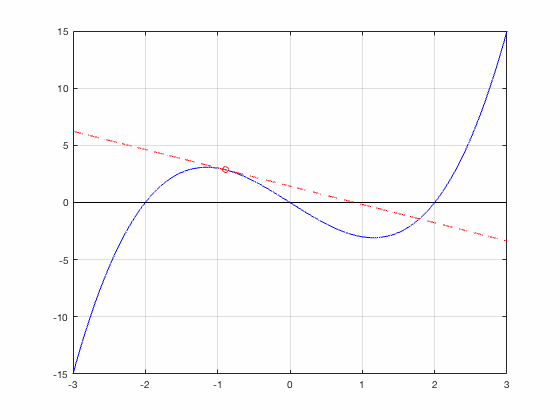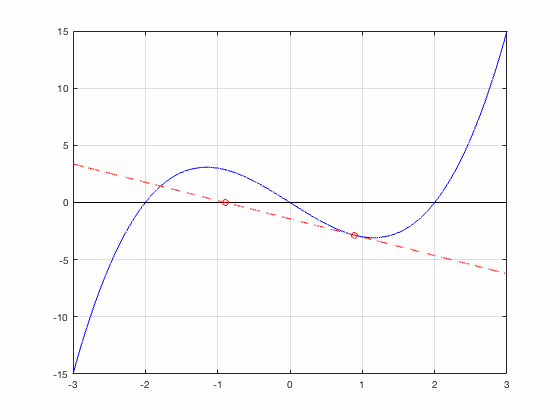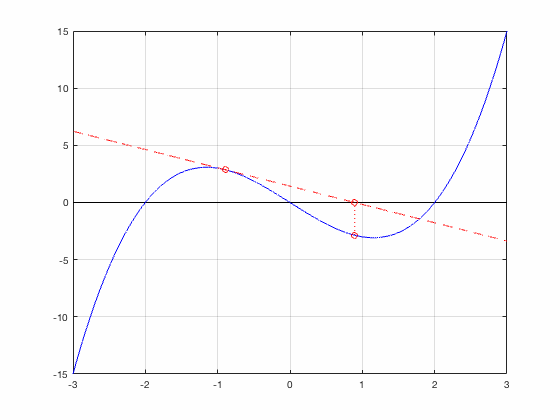
Newton's Method gets trapped in a 2-cycle
Taylor series converges to exp(x)
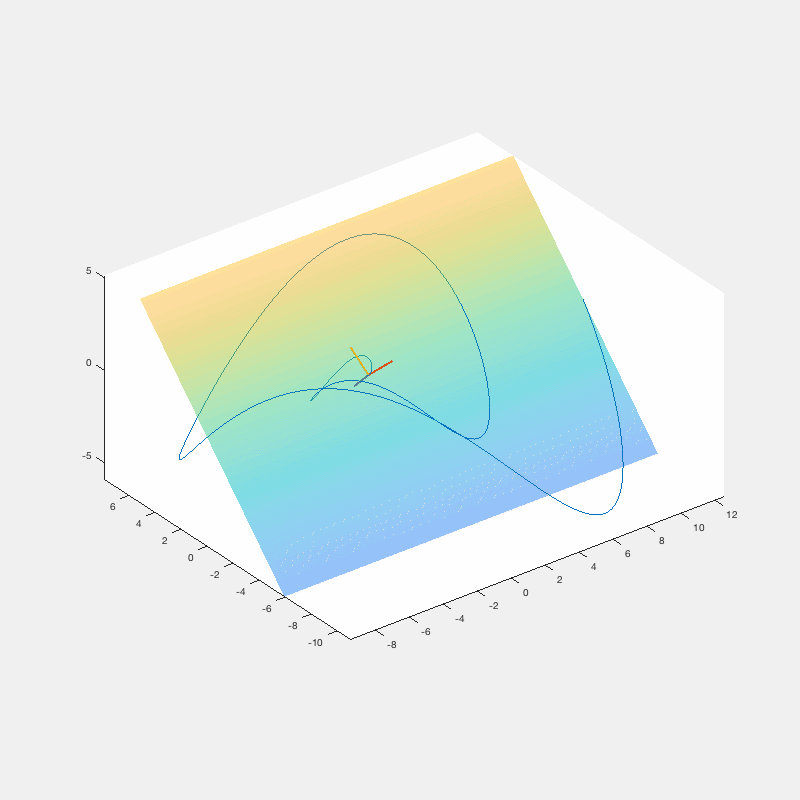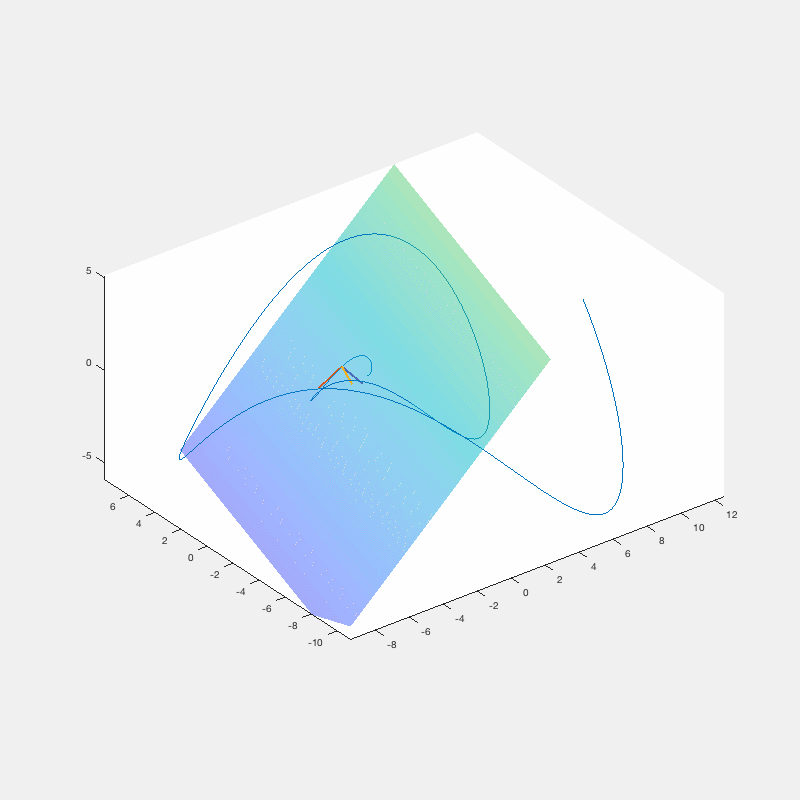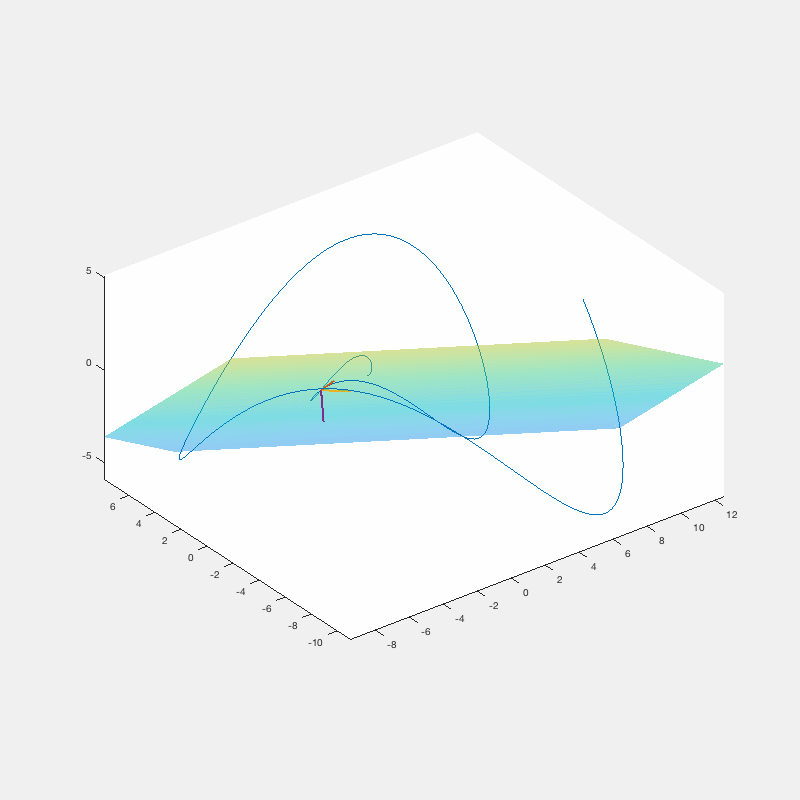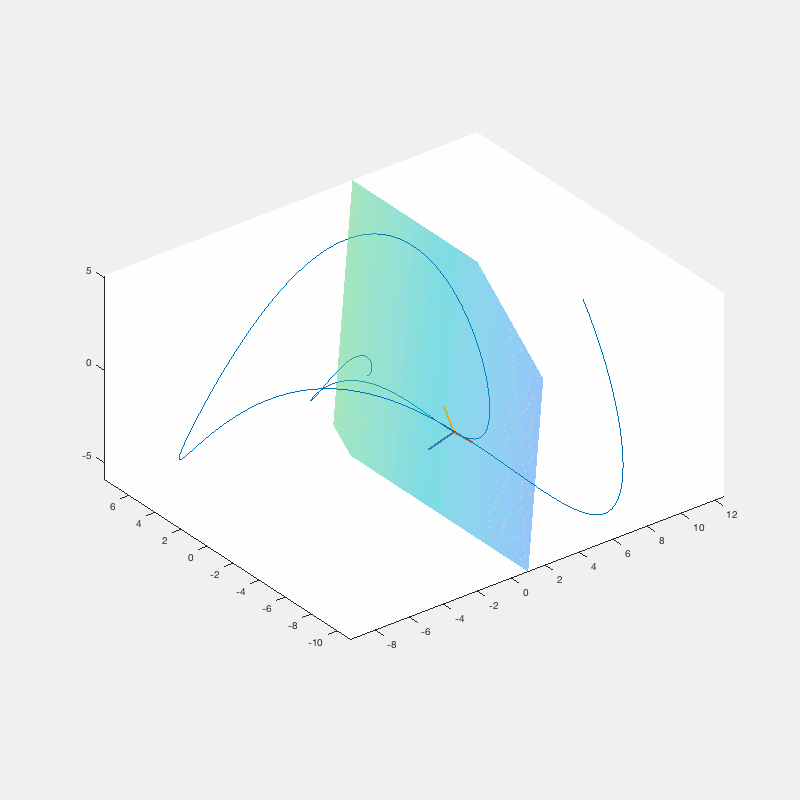
The Frenet-Serret or "TNB" frame ratchets around a space curve along with the osculating plane
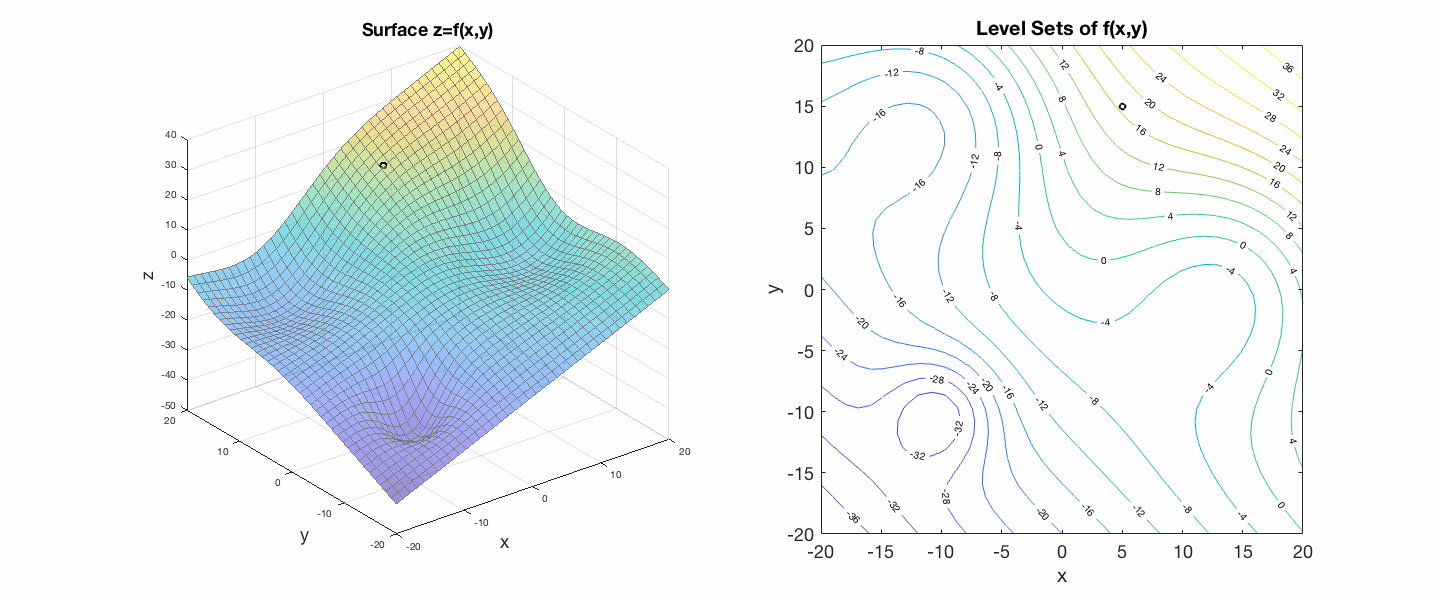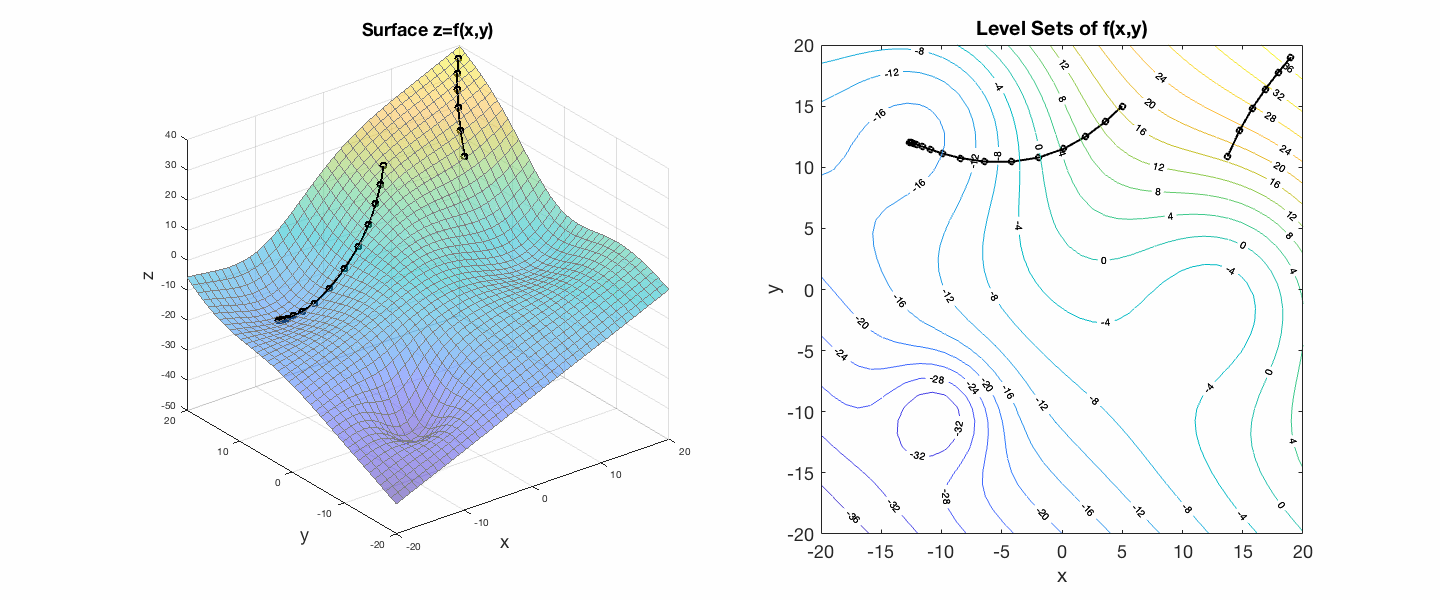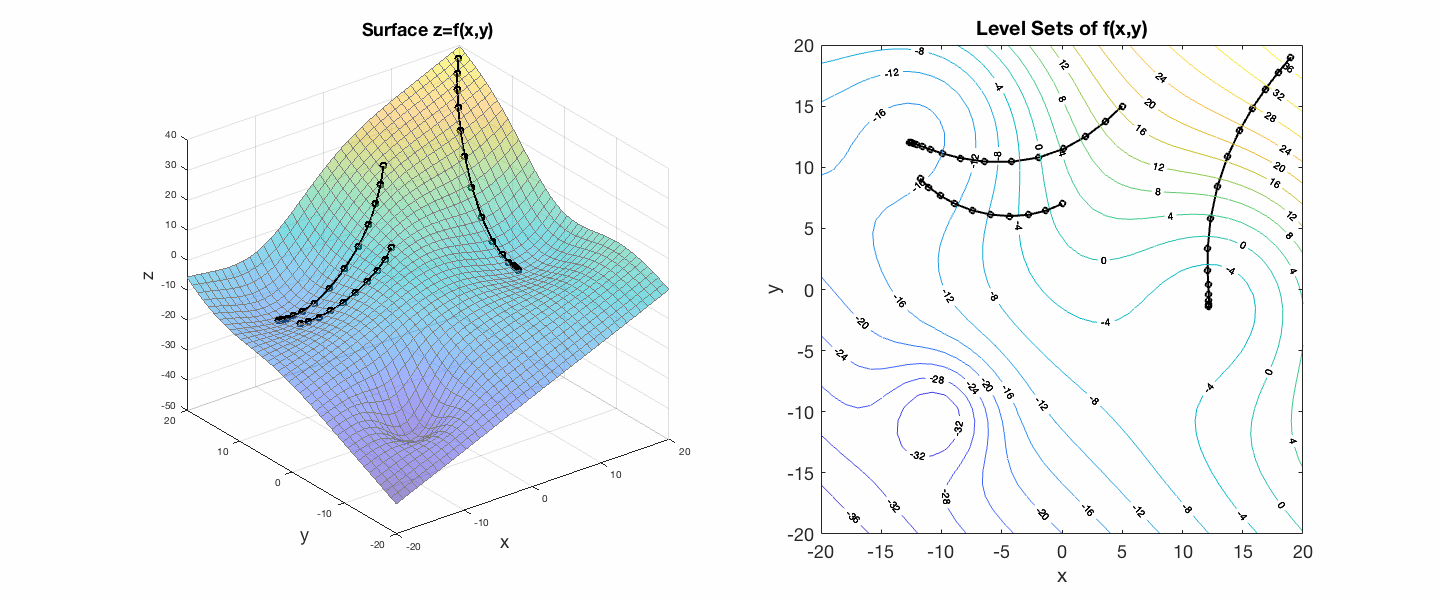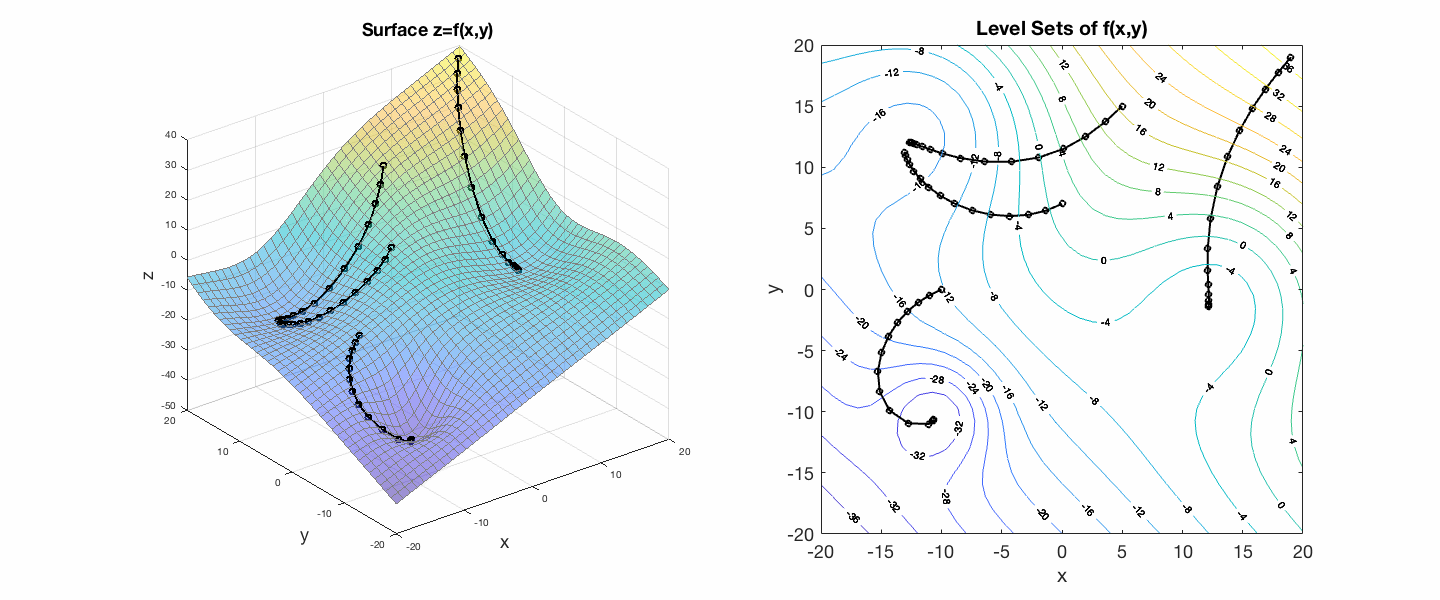
Gradient descent finds the local minima of a surface by moving "down" the gradient, stepping always perpendicular to the level curves of the surface
Calculus I – "When I say Derivative, you say slope!"
We've just computed our first derivative. Now, in our second example, we will use the intuition we've had since our first algebra class to compute the derivative of a linear function with no work at all! Of course, we must then confirm that our intuition is supported by the definition.
In the first example (not shown here), we practiced computing the derivative with the limit definition, with no preconceived notion of what might pop out, and then discussed the intuition behind the result. In this second example, we start with the intuitive answer, and then let the computation confirm our suspicions.
Calculus I – Interpreting Secant Slopes
In this clip, we compute the secant slope of an unknown function in the context of a car trip. By combining mathematical formulations, plain english description, and cartesian coordinate visualization, we discuss the physical interpretation of the slopes of a secant line.
We make use of the common sense intuition that a number of miles traveled divided by the time elapsed computes the speed. This paradigm is already well understood from "a train leaves the station" problems, but we now consider it geometrically. A key takeaway from this example is the insight that when the coordinate axes carry units, a slope computed in that coordinate system carries units as well.
Calculus III – TNB frame and Osculating Plane
Calculus is the math of motion and change. Using technology in the classroom can help calculus come to life in a way that is hard to communicate on a whiteboard.
In this clip, I give my students the chance to put their pencils down and observe the Frenet-Serret frame in motion.
We also use intuition to explain an interesting "flipping" behavior in the third example. By starting with simple cases, we develop the intuition necessary to explain this strange behavior. Including interesting cases in addition to run-of-the-mill examples is important for helping students develop a robust understanding of a new concept.
Calculus III – What's Up with Dot Products?
The first examples we give of a new concept are critical in equipping students with meaningful intuition. Here, we use a clever example to explore how the dot product of two vectors relates to the vectors' relative orientation.
A good example will not only serve students to grasp the concept initially, but will equip students with a solid litmus test to return to as new properties and theorems are unveiled.