
REACTION-DIFFUSION SYSTEMS
The diffusion of ligand and cytokines on intercellular spatial scales is critical to biological processes such as immune signaling, would healing, and embryonic cell differentiation. Diffusion in the body is limited to this scale, meaning the efficacy of diffusion as a delivery mechanism may act as a metric against which tissues measure themselves. Hypoxia in growing tumors due to insufficient diffusion of oxygen can lead to tumor angiogenesis, the first step in the cancer pathogenesis. In this way, diffusion, though a passive process, can play a crucial role in the organization of tissues, especially when considered in concert with reaction processes. Alan Turing famously outlined the idea of diffusion-driven instability in his 1952 paper "A chemical basis of morphogenesis."
CELLULAR AUTOMATA
Large systems of PDEs quickly become impractical as the the number of biological phenomena to be modeled and the dimensionality of the simulated space increase. Cellular Automata encode for state transitions governed by stochastic processes which PDE models can only approximate in the mean-field sense. Whereas PDEs consider continuous, real-valued densities which are deterministically evolved forward in time, the CA framework allows one to consider individuals explicitly. In some simple cases, CA models can be shown to upscale directly to PDE models, but in more complex cases, they can produce phenomena unavailable to deterministic modeling frameworks such as asymmetrical spread and stochastic fluctuations.
SPATIAL STRATEGIES OF THE INTERFERON RESPONSE
The production of interferons, a family of pro-inflammatory cytokines, is one of the earliest lines of defense the body has against novel viral infections. Interferons are responsible for a range of anti-viral actions, principal among them being the upregulation of anti-viral proteins in contacted cells. These proteins create an anti-viral environment in cells that can render healthy cells protected from infection and decrease the production of viral progeny from infected cells. The interferon response has studied in the past through the use of ODE and DDE models that neglect the spatial arrangement of cells.
We draw inspiration from classical epidemiological control strategies such as ring vaccination and contact tracing which target the susceptible individuals that are spatially proximal to infected individuals for profilaxis. In this way, we can see the interferon response as a warning signal to nearby cells that an infection is present, thus decreasing the availability of susceptible host cells for the infection and slowing or halting the spread.
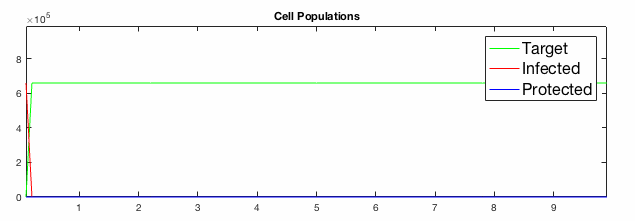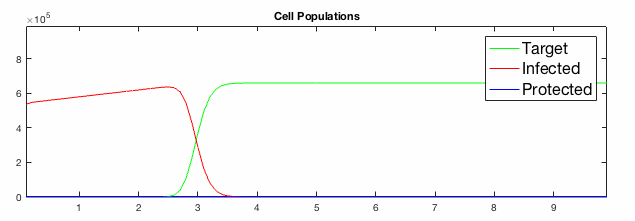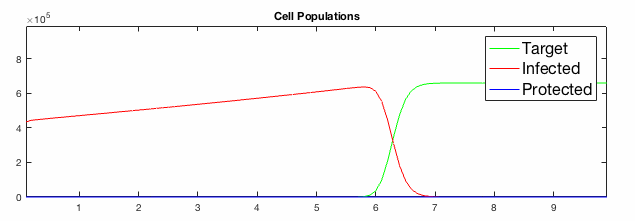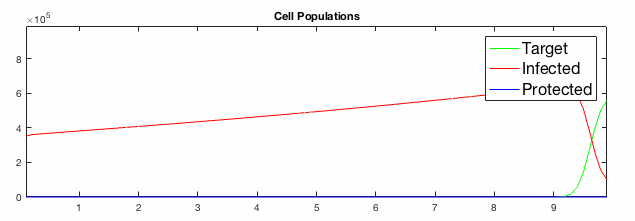
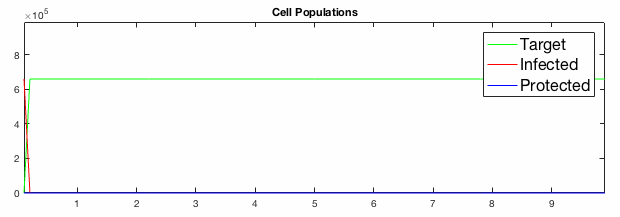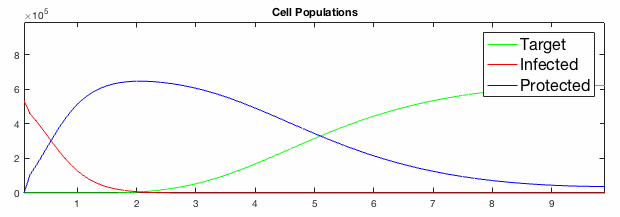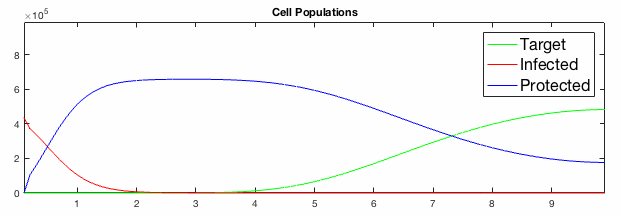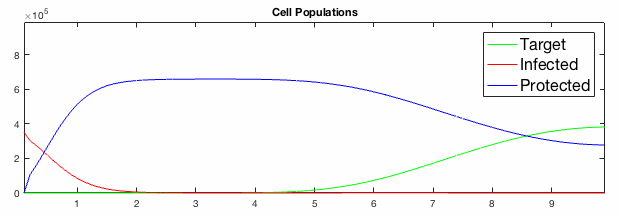
We have developed systems of Reaction-Diffusion PDEs to model viral infection with interferon response. The spread of infection across the 1D spatial domain occurs due to the diffusion of virus particles over the domain which is populated with stationary cell populations. The top simulation shows the uninhibited spread in the absence of interferon, whereas the bottom simulation shows the halted spread of infection due to the rapid decrease in susceptible cells.
Traveling wave analysis of this PDE system reveals how interferon signaling can act to reduce the speed of spread of infection.
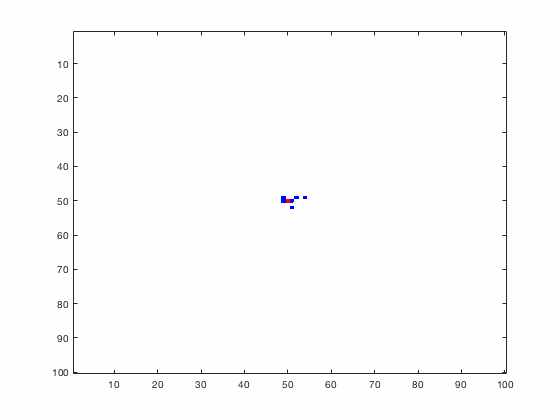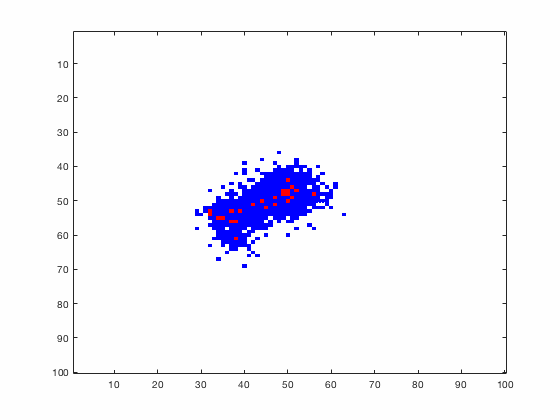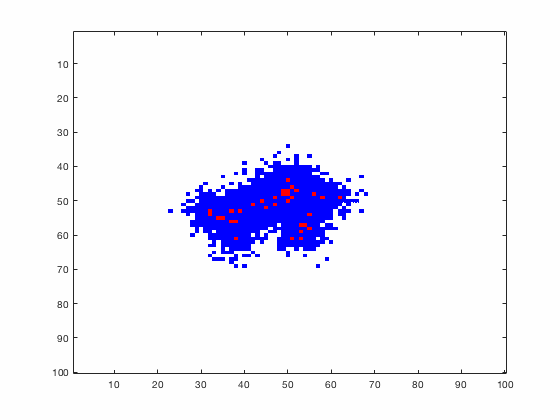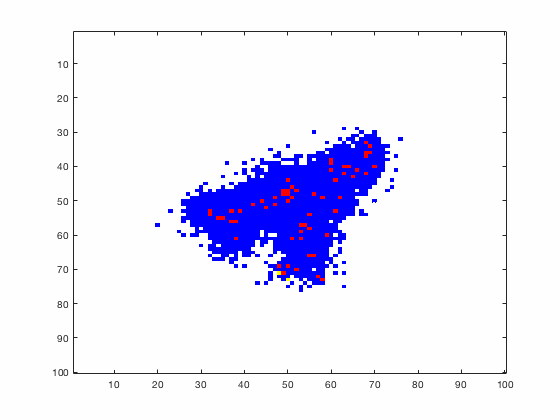
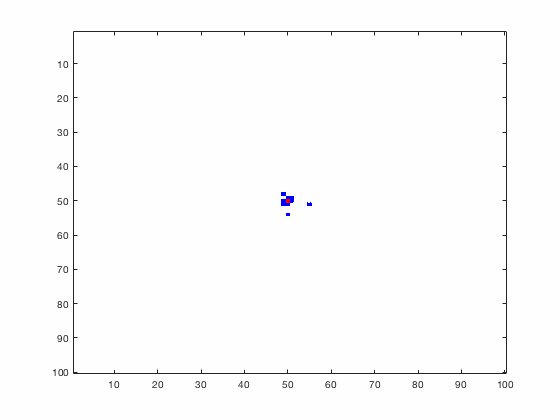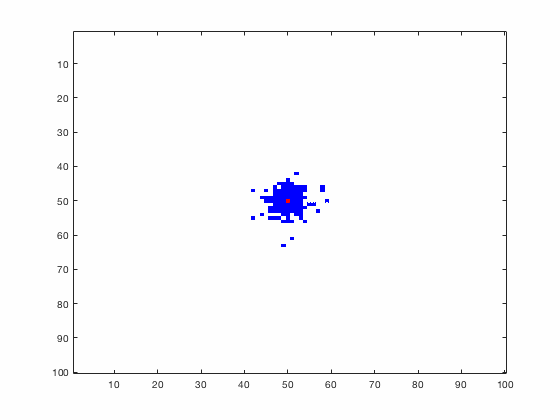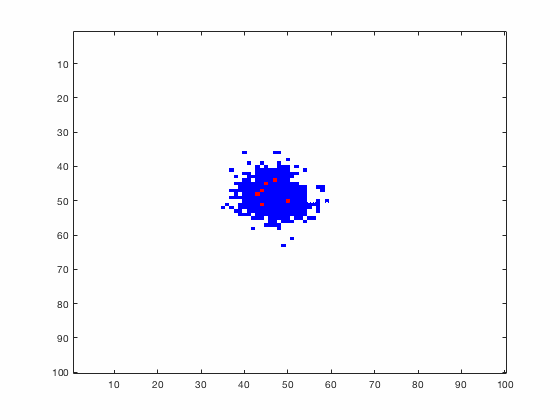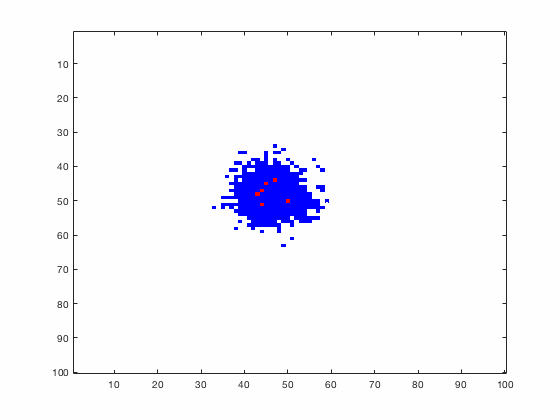
Large systems of PDEs rapidly become unwieldy as the number of phenomena and spatial dimension begin to increase. Cellular Automata (CA) models are composed of a grid of individuals and a set of rules that govern the stochastic changes in the state of the grid. In the simulations to the right, an initially healthy lattice of cells is gradually infected by a spreading viral infection. Between each time step, infected cells (red) produce both viruses and interferons, which diffuse to contact other nearby cells. Virus contact causes a cell to be become infected, while interferon contact causes a cell to become protected from infection (blue) and effectively inert. Simulations are shown for various levels of interferon production.
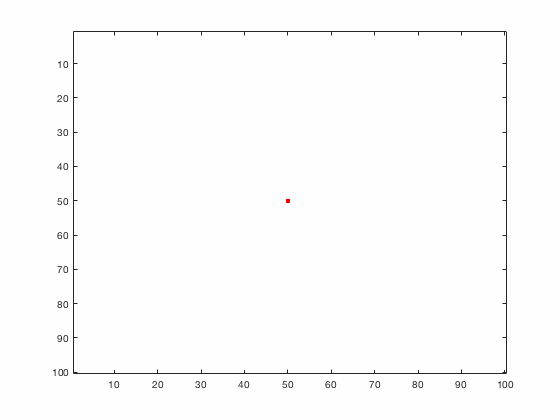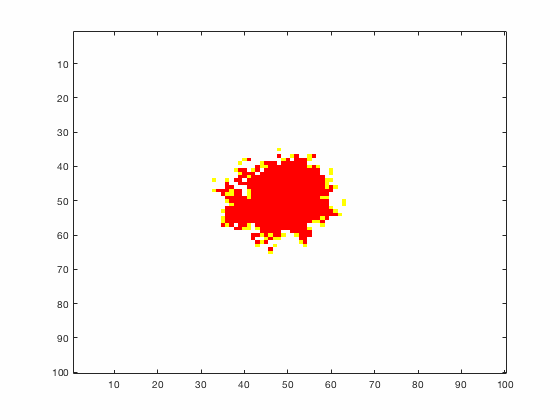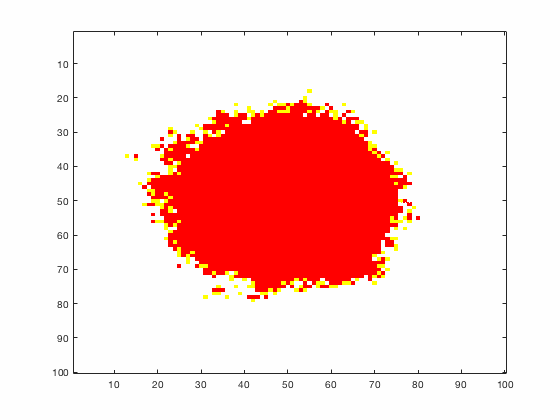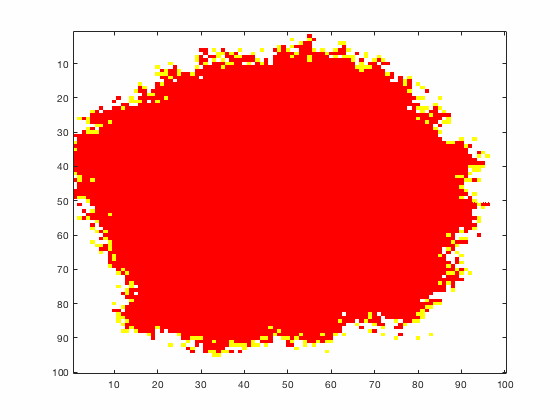
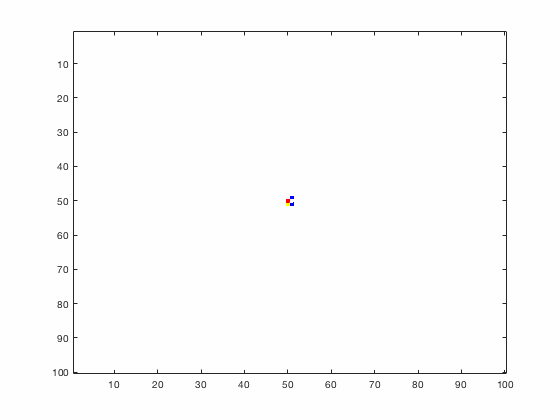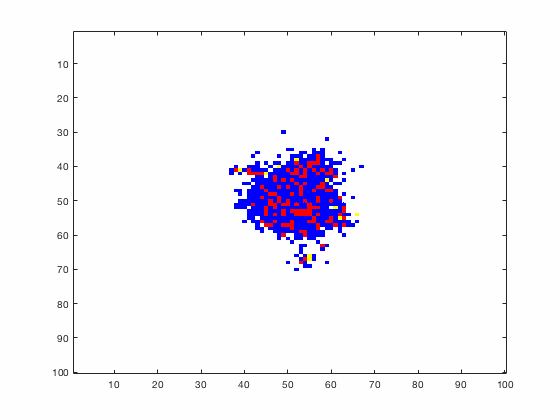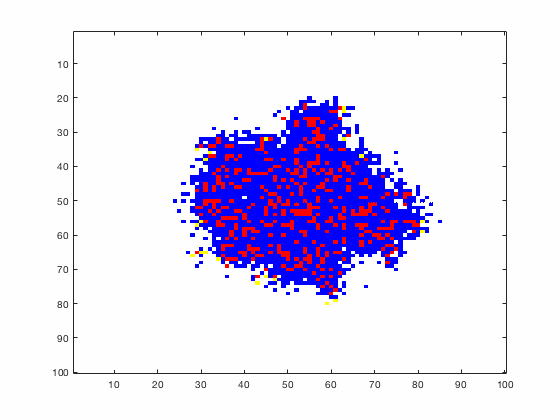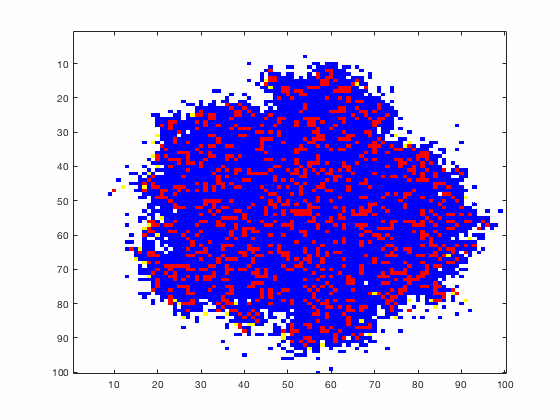
NON-MECHANISTIC EQUATION LEARNING
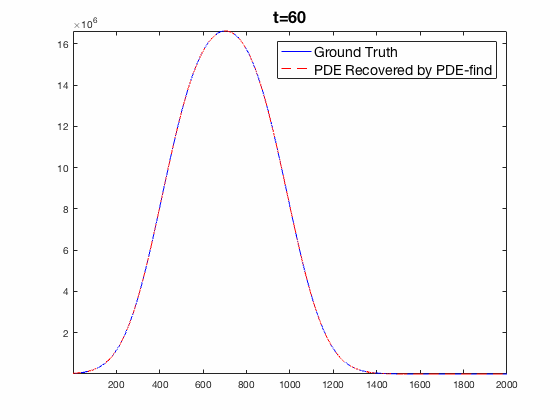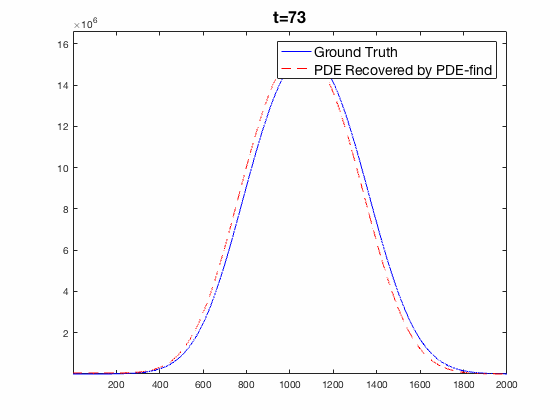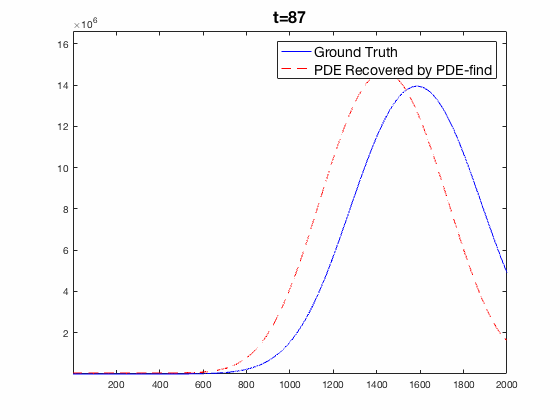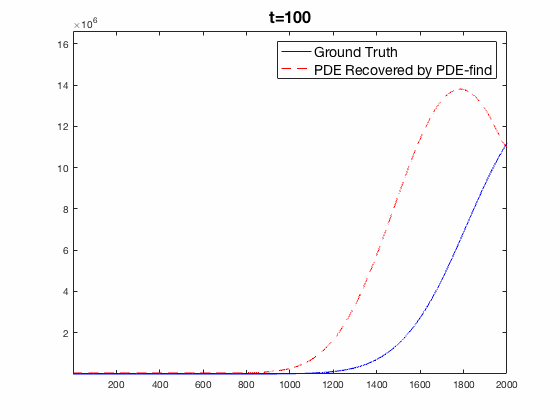
Traditional mechanistic modeling presupposes physical, statistical, or biological mechanisms that govern a system in order to find equations that can be fit to experimental data. For complex systems, the task of isolating key mechanisms may be difficult or impossible and may lead to several candidate models. Equation Learning (EQL) seeks to learn differential equations that govern a system from observational data with no mechanistic assumptions.
PDE-Find is a framework that employs sparse linear regression on a library of candidate model terms, allowing a vast number of candidate models to be compared in parallel.